The Beginning of a Journey into Mathematics
A bit of insight into what I'm thinking about at the start of this path.
Math is daunting.
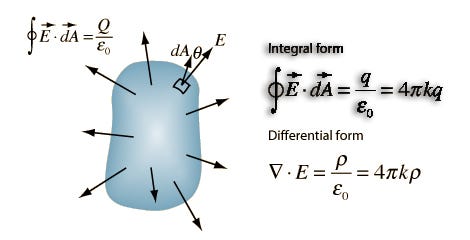
The various, complicated-looking symbols are scary. When I took AP Physics C, I came across surface integrals for the first time when calculating electric flux.
The textbook definitions had surface integrals in them, but in our calculations, we did everything to avoid them so we never learned how to calculate it, nor did we really have to understand it. I remember feeling like “Wow, that’s an advanced math concept we don’t cover at this level.” It felt so far away, and yet I’m now learning them exactly one year later, and… they’re not that bad. Now, looking back at some physics concepts, they seem much easier to understand, since the math and calculation aspect of understanding is not much of an obstacle. I notice that my ability to grasp the concepts has strengthened due to a better mathematical grasp.
There’s a moment of thrill I feel when I unlock a new math symbol, when I conquer a new piece of notation. The symbols are scary, but alluring.
My calculus course has helped me realize how developing a solid foundation in subjects not only speeds up the learning process significantly but is also so satisfying. It feels great when everything comes together and you can explain each level of complexity regarding a concept.
However, the process of developing a solid foundation in math is one that is quite involved.
Textbooks
Learning math is different from other subjects. You're different from CS majors and programmers, who are constantly coding, debugging, and looking up solutions and hacks to their problems. You’re different from Mech E majors who are strengthening their design skills through CAD and working hands-on in the makerspace, creating things. You’re different from people in the sciences such as chemistry or biology, who get a lot of their experience and expertise through wet lab.
A large part of studying mathematics is reading textbooks, which is something much less stimulating in comparison to the learning processes of the subjects I mentioned above. The process of learning math feels very… stoic. It’s a process that forces you to slow down and think more carefully. Words I associate with studying math are calm, collected, and thoughtful.
Reading a textbook in comparison to other methods of learning seems so mundane. Learning in a classroom setting with a teacher is more interactive and therefore arguably more enjoyable. Learning by using your hands and building something is more fun. Learning from videos can be more entertaining. Sometimes, hearing someone else explain it online just makes more sense. I’ve always been someone who learns better from videos than reading - things just click faster that way for me.
Like me, a lot of people I’ve spoken to dislike reading the textbook. They struggle to understand it and feel it’s too difficult to get through. Earlier this semester, I sat down to read Thomas Calculus, the textbook for my multivariable calculus class, back when I was grappling with the concept of partial derivatives and the chain rule. I sat there for 2 hours trying to understand the chapter and ended up walking away understanding only 30% of it. Frustrated and discouraged, I scrapped using the textbook and stuck to lecture videos/online videos.
When I started thinking about studying math more seriously, I knew that studying textbooks would be essential to becoming better at the subject. At one point, the level of the content would be too advanced, and there won’t be some smart Indian guy on YouTube to save me.
I decided to ask people much better than me at math how they approach textbooks. Surprisingly, the 4 people I asked all said the exact same things. They assured me that I’m not stupid for needing to read the same amount of text multiple different times. They mentioned how a math textbook can’t be read like a book - it’s a slow and diligent process. You have to sit down and meticulously go through each page. You have to interact with the material, solve problems, think critically about what’s presented, and prove what you see in the book on your own. And they said it gets easier over time, as your mathematical maturity grows. The more practice you have with reading textbooks, the better you get.
One morning, I opened up Chapter 15, which covered multivariable integration techniques, and worked through the content for a few hours. To understand it properly, I first reviewed simple integration content from Chapter 5 of the book and then came back to Chapter 15. At the end of my study, I had actually absorbed roughly 60-70% of the content. It took me a really long time, but it honestly felt so good - for the first time, I felt like I genuinely had a decent understanding of the material.
Reading the textbook is something that feels so different from typical activities in today’s society. I sound like a boomer, but it’s true. Reading a textbook slowly and deliberately felt like such a large contrast from the hyper-stimulating environment that technology creates for us. When reading, I oftentimes found that I would periodically lose focus within 5 minutes of reading. I couldn’t even concentrate for 5 minutes. I also found myself occasionally skimming lines, just not giving each part of the text proper attention because I wanted to get through the content quickly. I believe those are two main factors that prevent me from truly unlocking my ability to absorb content from a textbook. I’m currently still working on fixing those problems, but I already see an improvement in retention rate, and I’m slowly, very slowly, getting a little more efficient at reading as well. You can too.
I want to mention that doing difficult practices like these is not above me or you. Many times I’ve found myself justifying my inability to do certain things by saying “Oh yeah, that guy’s just smart. That’s why he can do it.” I excuse myself from doing hard things by belittling myself and claiming the activity is too far beyond my level. But it’s not.
Numbness
I feel very blind going on this journey. I don’t know what my future entails. A path of math (and CS) is so different from the path I had envisioned for myself in high school that my brain can’t process it - it’s numb. To be honest, I don’t even know if I care what lies at the end. I’m not sure if I even have a goal like “Oh I want to be good enough to go to grad school” or “Oh I want to be skilled enough to be a quant.” Perhaps this feeling of not having a goal comes from this feeling of numbness, since the idea of switching into a path in which I’m so behind and has so much uncertainty feels so overwhelming that my brain just shuts down.
What gives me some comfort is a newfound trust I’m developing in school curricula and structured courses. The math that I’ve attempted to self-study in the past never truly made sense until I actually took the class. What I described earlier about developing a solid foundation in calculus through my math class comforts me, because I know that the course will force me to learn the content so that I can perform on exams. No matter how difficult or stressful, I’ve always ended up doing okay in classes in the past, so why wouldn’t that trend continue?
I’m just following what I’m interested in and what challenges me. Maybe my brain shutting down is a good thing, because it stops analyzing and doesn’t resist me when I make small steps forward on the long road that is ahead of me. It’s immensely scary - I’m embarking on a journey towards a subject I feel I’m destined to fail the hardest in. And perhaps I will fail. But I guess that’s what makes life so exciting - doing something you never thought you would be able to do.
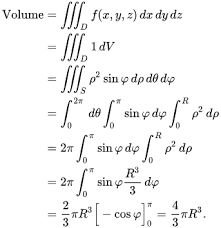
I recently read this speech by a guy named Paul Buchheit (the founder of Gmail). Particularly, he discussed the notion of 'Sic Parvis Magna', which, roughly, is Latin for "From Humble Beginnings, Great Destinations". Applied broadly, it feels like many people today don't care about those beginnings -- they're focused mainly on the ending. They want a unicorn, or a six-figure salary, or a big house with a nice view. It's fascinating how relevant this is in terms of education because most people view their studies as a means to achieve that 'glorious' ending. Conversely, while those aforementioned endings are totally valid, people who exclusively chase them lose track of their beginnings. In other words, they lose track of the 'why?'. I'm glad to see you grappling with that question of 'why?' as its a question people take their whole lives to answer. Taking that first leap is key and its good to see you jumping with courage. Your thoughts are also inspiration to me for being more cognizant & present in my learning process and putting together the big picture using the ideas I learned. Keep up the good thinking and I'm looking forward to the next post!
You are not alone! I feel like I'm diving into the deep end of physics and fighting so hard to keep myself from drowning. My peers, who decided this path for themselves a while ago, seem to be so far ahead of me. And I must keep reminding myself that it is not that I am stupid, I am simply less experienced (and not necessarily forever).
Take pride in the fact that you are moving away from a "grind-without-thinking" mentality to being more intentional about your education! When you finally make it to where you want to be, it will be so so worth it because you will know you have built yourself from the ground up (just think about how proud you would be of your current self one year ago!)